A review of Andro 55
Round Size Data
Early Round
Three fams kept pace for the opening week of the round (expo/no aggression phase), with 55 (Space Cats) having the planet lead as the opening week ended. Second was 59 (Special Forces) and third 56 (Fusion). 57 (Blonde) , 60 (Anon) and 58 (Crayons) rounded out the table.
Start of Aggression Wars
Once the one week wait for attacking was up each fam ended up in a war, with all six fams pairing off in a very honourable manner.
- Size Rank (2) 7759 (Special Forces) Declared on Size Rank (1) 7755 (Space Cats)
- Size Rank (3) 7756 (Fusion) Declared on Size Rank (4) 7757 (Blonde)
- Size Rank (5) 7760 (Anon) Declared on Size Rank (6) 7758 (Crayons)
- War 1 was won by 59 (special forces), which took them to the top of the size ranks
- War 2 was won by 56 (Fusion), which took them to 2nd in size
- War 3 was (eventually) won by 60 (Anon) , which took them to 4th in size.
56v57 was the shortest war, and 60v58 was the longest.
Growth Phase
During the next 150-ish Ticks was mostly econ-jumps (except for the ongoing 60v58 epic, and the 55 (Cats) v 57 (Blonde) war that kicked off just at the end of this phase.
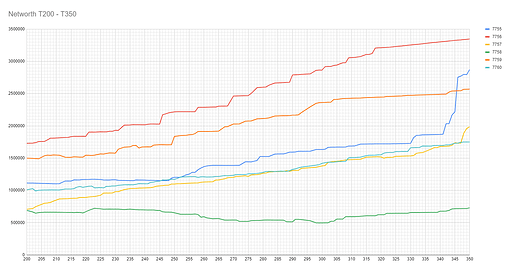
During this time 7756 (Fusion) had a NW (econ) lead as #1 fam by NW, and were able to extend this ahead of #2 by NW 7759 (Special Forces). 56 was able to have the advantage due to the shorter war with 57. The end of this phase is marked by 2 new wars, the aforementioned 55v57 and the clash of #1 and #2 in size and NW, 7759 (Special Needs) v 7756 (Fusion)
Mid-Round Wars
- War 4 7755 (Space Cats) Declared on 7757 (Blonde)
- T340 - T427
- Winner 7755 (+8 planets)
- NB: war determined by planet change analysis
-
Planet change may have been impacted by expos from 60 or either fam exploring blow-ups from 59v56

- War 5 7759 (Special Forces) Declared on 7756 (Fusion)
- T379 - T495
- Winner 7756 (+50 planets)
- NB: 7759 DOWN 68 planets as lots of planets were blown up and explored by 7760 and 7757
- War had 6 main phases
- Phase 1 - Early war 7759 declared and had early advantage
- Phase 2 - 7756 Fight back, planets get back to even
- Phase 3 - 7759 reclaim lead, raising to nearly 300 total planets before slowly start to lose
- Phase 4 - 7756 start to gain upper hand, but plenty of back and forth
- Phase 5 - 7756 dominate, but 7759 fight back, last ditch raids bring war back to even
- Phase 6 - 7759 capitulate and never recover, 7756 gain massive and get to over 320 planet, war ends

- War 6 7760 (Anon) Declared on 7755 (Space Cats)
- T505 - T527
- Winner 7760 (+17 planets)
- NB: war determined by planet change analysis
- Appears to be a short “war” mostly around a few system grabs by 7760

End of Round Wars and Jumps
7760v7755 could nearly be called an EOR war, but was left in mid-round due to length (and that both 7755 and 7760 were then involved in other actual EOR war with 7757 and 7759 respectively)
- War 7 7757 (Blonde) Declared on 7755 (Space Cats)
- T528 - T628
- Winner 7757 (+34 planets)
- NB: war determined by planet change analysis
- Was a rematch of war #4

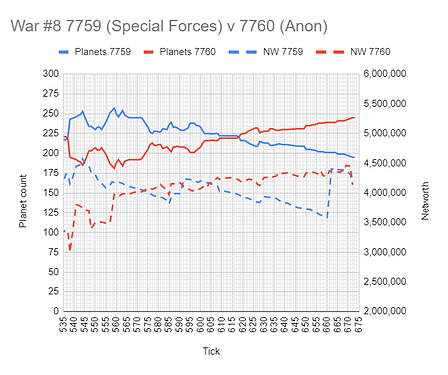
- War 8 7759 (Special Forces) Declared on 7760 (Anon)
- T536 - T673 (EoR)
- Winner 7760 (+24 planets)
- Planets lost by 7759 right up to last tick of the round

EoR Jumps (NW)
Two Fams had an EoR Jump (the two not involved in any EoR wars)
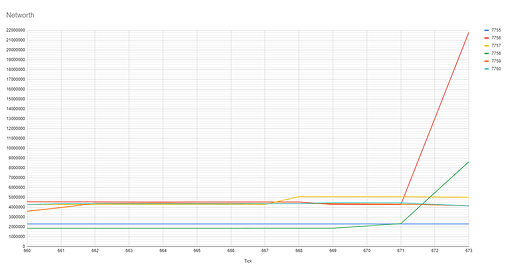
- 7756 (Fusion) jumped from 4,272,071 NW to 21,796,366 (+17,524,295 NW)
- 7758 (Crayons) jumped from 2,333,008 NW to 8,622,149 NW (+6,289,141 NW)
This put Fusion #1 in NW and Size at end of the round, with Crayons #2 in NW, but Anon #2 in size
War Stats
- #1 Size: 7756 (Fusion) Fought in two wars with a win record 2-0, defeating 7757 (Blonde) and 7759 (Special Forces)
- #2 Size 7760 (Anon) fought in three wars with a win record 3-0, defeating 7758 (Crayons), 7755 (Space Cats) and 7759 (Special Forces)
- #3 Size 7759 (Special Forces) fought in three wars with a win record 1-2, defeating 7755 (Space Cats), but losing to 7756 (Fusion) and 7760 (Anon)
- #4 Size 7757 (Blonde) fought in three wars with a win record 1-2, defeating 7755 (Space Cats II) in the rematch, but losing to 7756 (Fusion) and 7755 (Space Cats I)
- #5 Size 7755 (Space Cats) fought in three wars with a win record 1-2, defeating 7757 (Blonde I) in the first match, but losing to 7759 (Special Forces) and 7757 (Blonde II)
- #6 Size 7756 (Crayons) fought in only 1 war with a win record of 0-1, losing to 7760 (Anon)
War Comments
- 7759 (Special Forces) was only fam to fight other top 3 fams at time of war
- Declared on 7755 when was 1v2 in size
- Declared on 7756 when was 1v2 in size
- Declared on 7760 when was 2v3 in size
- 7760 (Anon) only fam to win 3 wars, and in each case against a fam bigger than them
- Defeated 7758 (Crayons) when 6th and crayons were 5th by size
- Defeated 7755 (Cats) when 4th and Cats were 3rd by size
- Defeated 7759 (Special Forces) when 3rd and Special Forces were 2nd by size
- 7759 (Special Forces) were only fam to lose when declaring (and lost 2 wars after declaring). All other wars were won by the side declaring (or attacking first)
Alternative Scoring
| Rank | Family | War Score | Current Elo | Current Size Rank | Current Planet Count | Current Networth |
|---|---|---|---|---|---|---|
| 1 | 7756 | 2,180 | 1,480 | 1 | 314 | 21,796,366 |
| 2 | 7760 | 2,311 | 1,121 | 2 | 245 | 4,135,009 |
| 3 | 7759 | 1,938 | 1,089 | 3 | 195 | 4,146,508 |
| 4 | 7757 | 588 | 979 | 4 | 181 | 5,018,017 |
| 5 | 7755 | 2,611 | 769 | 5 | 132 | 2,298,069 |
| 6 | 7758 | 489 | 439 | 6 | 102 | 8,622,149 |
Elo Rating
Results show similar results to Size, but results over time give an indication of econ strength (NW). Also results over time clearly show improvement of 7760 over whole round, and decline of 7755 and 7759 after losses.
War Score
War score is based on the calculations for victory in Clan Wars. Over course of last few rounds it has shown as a good indicator for war winner prediction, as well as indicator for most war like family. War score is shown here for information purposes. All war summaries use potential war score (war score calculated at start of war) to determine odds of declaring fam winning war.
Declaring Fam Win % = 1- [Fam(Decl) Potential score / Sum of both potential score]
Notes on Elo Rating
Elo rating is a system (normally used for games involving 2 players) that attempts to rate a players expected performance based on past performances. I have adapted it for use in IC in 3 ways. First is to give a running score based on NW ranking, second the same for Size ranking, and lastly as a rating on war performance.
Ratings are biased towards war performance.
The Elo rating should show expected outcomes in future ticks, i.e. high Elo should indicate that a fam will be higher ranked in Size and NW rankings, and more likely to win any war when compared to a lower Elo rated fam. Is a good indicator of war performance. Elo ratings could be used to later determine player ratings.
This was calculated using the standard Elo calculation, modified slightly
Elo(n) = Elo(n-1) + k(size) * (S(size) - E) + k(NW) * (S(NW) - E) + dElo(War)
Where:
Elo(n) = Elo rating this tick
Elo(n-1) = Elo rating last tick
k(Size) = Elo coefficient for Size ranking (currently set to `5`)
k(NW) = Elo coefficient for NW ranking (currently set to `5)
S(Size) = Modified Size Rank result this tick
S(NW) = Modified NW Rank result this tick
E = Expected result based on Elo rating
The modified ranks are calculated by dividing the actual rank by the number of families in the galaxy less 1
S = Rank / [Num(fam) - 1]
E is calculated based off the last ticks Elo for the fam, and the average Elo for all fams in the galaxy
E = R1 / (R1 + R2 )
Where
R1 = 10^(Elo(n-1) / 400)
R2 = 10^(MeanElo / 400)
The dElo(War) is the change (delta) in Elo ratings from wars. It is calculated as follows (Standard Elo calculation)
Elo(n) = Elo(n-1) + k(war) * (S - E)
Where
Elo(n) = Elo rating this tick
Elo(n-1) = Elo rating last tick
k(war) = Elo coefficient for wars (currently set to 50)
S = Result of war (Win S = 1, Loss S = 0)
E = Expected result based on Elo rating
E is calculated similar to NW and Size ranking Elo, but uses the Elo of the 2nd fam in the war
E = R1 / (R1 + R2 )
Where
R1 = 10^(Elo(Fam1 n-1) / 400)
R2 = 10^(Elo(Fam2 n-1) / 400)
Elo(n) is worked out for each fam (R1 and R2 are swapped for each fam)
Calculation for War Score
Potential War Score = modifier * Size Score + NW(modified) Score
Where
Modifier = [1- % difference in planets] if difference is more than 15%
Size Score = 10 * [ Number of Planets of fam at start of war / Number of planets of other fam at start of war]
NW(modified) Score = 10 * [NW of fam at start of war less NW due to planets / NW of other fam at start of war less NW due to planets]
After war ends, the final score is determined based on who won the most planets, and how many planets they won
Final Score = Potential Score * Winning Modifier * Farming Modifier
Where
Winning Modifier = 100% if gain more planets (Win) or 25% if lose more planets (Lose)
Farming Modifier = 100% if less than 15% of planets lost, 75% of 15-25% of planets lost, 50% if 25-35% of planets lost, 25% if 35-50% of planets lost, 0% if more than 50% of planets lost









 Great work
Great work  and gg everybody.
and gg everybody.